Conway’s Game of Life in Logic Gates
What is the minimum number of logic gates (restricted to AND, OR, and NOT) needed to implement a cell in Conway’s game of life? An automated tool had arrived at the rather pessimistic number of 1091, and I could do better. Here’s my thought process and the answer I got.
Versions 1 and 2: Adders
I did some quick arithmetic and said I could do it in 75 gates. By the time I sketched out the circuit there were only 61. This was the circuit picked up by poslathian. It works by summing the eight adjacent cells using four half adders, then summing the four resulting two bit numbers using a two bit adder. The carry bits from the two bit adders are ORed together, if the resulting value is true then there are four adjacent live cells and this cell must die. Otherwise we look at the two bit result and the current state of the cell to compute the result. Here is the schematic: Life in 61 gates [20 kb].
Why so many gates? It turns out that using adders and half adders consumes a lot of gates when you have to construct XOR gates out of simpler gates. Two’s complement arithmetic is convenient and easy to understand but takes up space on the circuit. There was also some redundancy that I caught in the circuit — when adders are cascaded input to output, only one adder in each chain can signal a carry at the same time. I was able to simplify the carrying circuit, eliminate full adders, and reduce the gate count to 49. Here is the schematic: Life in 49 gates [18 kb].
Version 3: Sorting Network
I saw a schematic on with a lower gate count than mine, so I tried to figure out how it worked. It took pairs of inputs and instead of adding them, it sorted them. Sorting two binary inputs is easy: just use one OR gate and one AND gate. This operation is also called “compare and exchange”. I did a search online to try and find the smallest possible 8 item sorting network. One web page claimed that the smallest 8 item sorting network is known, which encouraged me, and I found a sorting network for the odd-even mergesort that was better than the sorting network I came up with on my own (which also used mergesort). The sorting network I found uses 19 compare and exchange operations.
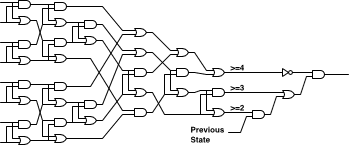
Once the input is sorted you have a signal for when there are at least two, three, and four adjacent cells active. The sorting network generates signals we are not interested in, allowing seven gates to be eliminated. This leaves 31 gates, and four more complete the circuit. The final total is 35 gates. A higher quality version of the schematic is available here: Life in 35 gates [19 kb].
So what?
Implementing Conway’s game of life is simple and straightforward, but producing a small circuit for it requires some more sophisticated thinking. Who would have thought that a mergesort algorithm would be optimal? I’m interested in other people’s results, as some people have discussed attacking the problem with automated tools and brute force techniques.